İŞLEM KOLAYLIKLARI
1)
1) 5 ile
çarpmak: Bir sayıyı 5 ile
çarpmak için 10 ile çarpıp yarısını almak yeterlidir
Örnek:
Örnek:
2) Bir
sayıyı 
ile çarpma: Sayı 2 ile çarpılır 10 a
bölünür.
Örnek:
3)
3) 9 ile bölümden kalanın bulunması: Verilen sayının rakamları toplanır, elde
edilen sayının tekrar rakamları toplanır. En son elde edilen toplam 9 dan küçük
oluncaya dek rakamlar toplanır, sonuçta elde edilen 9 dan küçük rakam kalan
sayıyı verir.
Örnek: 8256
nın 9 ile bölümünden kalan nedir?
kalan 3 tür.
Örnek:679345
sayısının 9 ile bölümünden kalan nedir?
kalan 7
dir.
4)
4) 11 ile çarpma : Verilen sayının birler basamağı ile onlar basamağı toplanır
birler basamağındaki rakamın soluna
yazılır. Elde var ise onlar basamağına eklenir ve onlar basamağı ile yüzler
basamağı toplanır.
Örnek: 57x11=627
Örnek: 4868x11=53548
8 yazılır. 6+8=14, 8 in soluna 4
yazılır. 8 e 1 eklenir 9 ile 6 toplanır. 9+6=15 yüzler basamağına 5 yazılır.
Elde olan 1 ile 4 e eklenir. 5 ile 8 toplanır. 5+8=13 , 3 binler basamağına
yazılır, elde 1 kalır. 1+4=5 olup toplanacak başka rakam kalmadığından on
binler basamağına yazılır.
5)
5) Sonu 5 olan sayıların karesini almak: Beşin solundaki rakam 1 artırılır.
Onlar basamağı ile çarpılır. Çarpım yazılır ve çarpımın sağına 25 yazılır.
Örnek: (45)² = ?
4+1=5 olup, 4.5=20 dir. 20 nin
yanına 25 yazılır.
(45)² = 2025
Örnek: (135)²=18225
13+1=14
13x14=182
25 in soluna 182 yazılır.
6)
6) a ve b birer gerçek sayı ise,
(a+b)²=a²+2ab+b²
özdeşliğinden yararlanarak iki basamaklı sayıların karesi
kolay alınabilir.
Örnek: (34)²=?
a=3 , b=4 gibi düşünülerek, önce b²=4²=16 bulunur.6 birler basamağına
yazılır.
2.a.b = 2.3.4 = 24 bulunur. 1+24 = 25 olup onlar basamağına 5 yazılır. Elde
2 kalır. a²=3²=9 ile 2 toplanır. 9+2=11
olup, yüzler basamağına 1 ve binler basamağına 1 yazılır.
(34)²=1156 dır.
Örnek: (86)²=7396
b²=6²=36 Birler basmağına 6
yazılır. Elde kalan 3, 2.a.b=2.8.6= 96 ile toplanır. 96+3=99, 9 onlar
basamağına yazılır. Elde kalan 9, 8²=64 ile toplanır. 64+9=73 ve 3 yüzler
basamağına, 7 binler basamağına yazılır.
7)
7) a ve b gerçek sayılar olmak üzere,
a² -
b²=(a - b) (a + b)
özdeşliğinden yararlanarak işlemler kolaylıkla sonuçlandırılabilir.
Örnek: 1999² - 1= (1999 - 1) (1999 + 1)
=
1998.2000 = 3996000
Örnek: 78² -
57² = (78 - 57) (78 + 57)
=21.135
= 2835
Örnek: 1de n ye
kadar olan tek doğal sayıların toplamı n² dir. Buna göre 68 ile 136 arasındaki
tek sayıların toplamı kaçtır?
Çözüm: 136 ya kadar 68 tane tek doğal sayı vardır. 68 e kadar olan 34 tek doğal
sayılar bu toplamın içinde yoktur. Buna göre;
68² - 34² = (68 - 34) (68 + 34)
= 34.102 = 3468
Örnek:
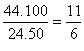
8)
8) 9 ile çarpma: Verilen sayı 10 ile çarpılır. Sonuçtan kendisi çıkarılır.
Örnek: 38.9= 38.10 - 38 = 380 -38=342
Örnek: 148.9 = 148.10 - 148 =1480 -148 =1332
9)
9) n,k gerçek sayılar olmak üzere bir
sayının k.10ⁿ biçiminde yazılmasına o sayının üslü biçimde gösterimi
denir.
Örnek:
Örnek:
Örnek:
SAYILARDA MUTLAK DEĞER
olur.
Sayı ne olursa olsun pozitif değeri mutlak değerdir.
Tanım: x bir gerçek sayı olmak üzere;
Örnek:
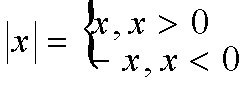
Örnek: a,b gerçek sayılar ise;
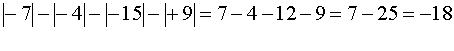
İşleminin sonucu nedir?
Çözüm:
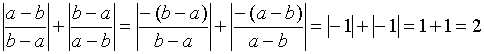
Örnek:a bir gerçek sayı ise 
ifadesinin değerini bulunuz.
Çözüm: 
alınır. (Tanım)
Örnek: 
nın en küçük değeri 0 dır. A=3x-1, B=3x-a+2 ve A+B nin
mutlak değeri en küçük ise a tam sayısının değeri kaçtır?
Çözüm:
dir.